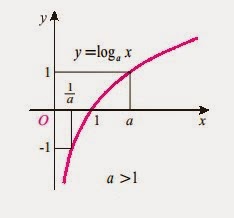Կոորդինատային մեթոդ և վեկտորներ
Դեկարտյան կոորդինատների համակարգ ամենահասարակ և ամենահաճախ օգտագործվող կոորդինատային համակարգն է հարթությունում և տարածությունում։Դեկարտյան կոորդինատները ներմուծվել են ֆրանսիացի գիտնական Ռենե Դեկարտի կողմից 17-րդ դարում։ Այն ներմուծելուց հետո առաջին անգամ հնարավոր եղավ կապ ստեղծել Էվկլիդեսյան երկրաչափության և հանրահաշվի միջև։ Դեկարտյան կոորդինատների ներմուծումով հնարավոր եղավ երկրաչափական պատկերները նկարագրել դեկարտյան հավասարումներով՝ հանրահաշվական հավասարումներով, որոնք ներառում են պատկերին պատկանող կետերի կոորդինատները։ Օրինակի համար, 2 շառավողով շրջանագիծը կարելի է ներկայացնել որպես այն բոլոր կետերի բազմությունը, որոնց կոորդինատները բավարարում են հետևյալ հավասարմանը՝ x^2 + y^2 = 2^2։
A(x,y)
B(x,y) Օրինակ նշենք A(-3;2) և B(2;-3) կետերի կորդիատները A կորդինատի -3-ը պատկանում է x-ների (աբցիսների) առանցքին, իսկ 2 պատկանում է y-ների (օրդինատների) առանցքին, իսկ B կորդինատի 2-ը պատկանում է x-ների (աբցիսների) առանցքին, իսկ -3-ը պատկանում է y-ների (օրդինատների) առանցքին
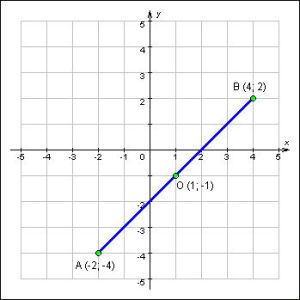
A(-2;-4) և B(4;2) AB հատվածի միջնակետի կորդինատը (այդ կետը նշանակենք Օ-ով) գտնելու համար պետք է օգտագործել հետևյալ բանաձևը Օ((X1+X2 )/2;(Y1 +Y2 )/2) => O (1;-1)
A և B կետերի միջև հեռավորությունը որոշելու համար օգտագործում են հետևյալ բանաձևը այսինքն, եթե A(-2;-4) և B(4;2) ապա AB հատվածի երկարությունը հավասար կլինի = :
Կորդինատների Օxy ուղղանկյուն համակարգում r շառավղով և C(X0 ;Y0) կենտրոնով հավասարումն է՝ (X-X0)^2+(Y-Y0)^2=r^2 Մասնավորապես, r շառավղով և կորդինատենրի 0(0;) սկզբնական կենտրոն ունեցող շրջանագծի հավասարումն է ՝ X^2+Y^2=r^2:
Հավասար վեկտորներն ունեն համապատասխան հա- վասար կոորդինատներ։ Եվ հակադարձը՝ եթե երկու վեկտորների համապատասխան կոորդինատները հավասար են, ապա այդ վեկտորները հավասար են։
Աստիճանային ֆունցկիա
Աստիճանային ֆունկցիա կոչվում է հետևյալ բանաձևով տրված ֆունկցիան, որտեղ a-ն 0-ից տարբեր թիվ է` f(x) = xa
Բնական ցուցիչով ֆունկցիան աստիճանային ֆունկցիան շատ հատկություններով նման է գծային ֆունկցիային, երբ n-ը կենտ է, և քառակուսայինին` երբ n-ը զույգ է:
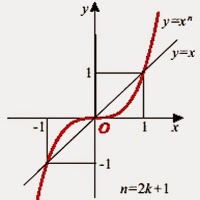
n-ը կենտ դեպքում, ֆունկցիայի հատկությունները`
1. Ֆունկցիայի որոշման տիրույթն անբողջ թվային առանցքն է` D(f) = (-∞; ∞)
2. Ֆունկցիան կենտ է` f(-x) = (-x)n = -xn = -f(x), հետևաբար` ֆունկցիայի գրաֆիկը համաչափ է կոորդինատների սկզբնակետերի նկատմամբ:
3. Ֆունկցիան ունի մեկ զրո` f(0) = 0
4. Ֆունկցիան դրական է, երբ x պատկանում է (0; ∞) և բացասական` երբ x պատկանում է (-∞; 0):
5. Ֆունկցիան աճում է ամբողջ թվային առանցքի վրա:
Ենթադրենք` x1 < x2 և համոզվենք, որ f(x1) < f(x2): Դիտարկենք երեք դեպք`
ա) 0 ≤ x1 ≤ x2, ապա ըստ բնական ցուցիչով աստիճանի հատկության` f(x1) ≤ f(x2):
բ) x1 < 0 ≤ x2, ապա ըստ 4-րդ հատկության` f(x1) < 0 ≤ f(x2):
գ) x1 < x2 ≤ 0, ապա –x1 > -x2 ≥ 0, ուստի f(-x1) > f(-x2), որտեղից, ֆունցկիայի կենտությունից հետևում է, որ` -f(x1) > -f(x2), => f(x1) < f(x2):
- Ֆունկցիայի արժեքների բազմությունը ամբողջ թվային առանցքն է` E(f) = (-∞; ∞):
Հետևություն` ֆունկցիան սահմանափակ է և չունի մեծագույն ու փոքրագույն արժեքներ:
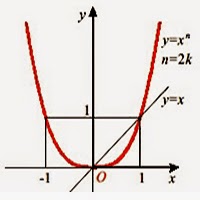
n-ը զույգ դեպքում, ֆունկցիայի հատկությունները`
1. Ֆունկցիայի որոշման տիրույթն անբողջ թվային առանցքն է` D(f) = (-∞; ∞)
2. Ֆունկցիան զույգ է` f(-x) = (-x)
n = x
n = f(x), հետևաբար` ֆունկցիայի գրաֆիկը համաչափ է կոորդինատների սկզբնակետերի նկատմամբ:
3. Ֆունկցիան ունի մեկ զրո` f(0) = 0
4. Ֆունկցիան դրական է, երբ x ≠ 0:
5. Ֆունկցիան նվազում է (-∞; 0] և աճում [0; ∞) միջակայքերում:
6. Ֆունկցիայի փոքրագույն արժեքը 0-ն է, որն ընդունում է 0 կետում: Ֆունկցիան չունի մեծագույն արժեք:
7. Ֆունկցիայի արժեքների բազմությունը ոչ բացասական թվերի բազմությունն է` E(f) = [0; ∞)
Օրինակ՝

Հատուկ առանձնացվում է այն դեպքը, երբ որպես աստիճանի հիմք հանդես է գալիս  թիվը։ Այդպիսի ֆունկցիան կոչվում է էքսպոնենտային (իրական կամ կոմպլեքս)։
թիվը։ Այդպիսի ֆունկցիան կոչվում է էքսպոնենտային (իրական կամ կոմպլեքս)։
Ցուցչային ֆունկցիայի սահմանումը
Դիցուք  -ն ոչբացասական իրական թիվ է, իսկ
-ն ոչբացասական իրական թիվ է, իսկ  -ը ռացիոնալ թիվ՝
-ը ռացիոնալ թիվ՝ ։ Այդ դեպքում
։ Այդ դեպքում  -ը որոշվում է հետևյալ կանոններով՝
-ը որոշվում է հետևյալ կանոններով՝
- Եթե
 , ապա
, ապա ![a^x= \sqrt[n]{a^m}](https://i2.wp.com/upload.wikimedia.org/math/5/9/b/59bb51c4bbf9bb3f0c594b414317e599.png) ։
։
- Եթե
 և
և  , ապա
, ապա  ։
։
 -ի արժեքը որոշված չէ։
-ի արժեքը որոշված չէ։- Եթե
 և
և  , ապա
, ապա ։
։
 -ի արժեքը
-ի արժեքը  ,
,  -ի դեպքում որոշված չէ։
-ի դեպքում որոշված չէ։
Ցանկացած  իրական ցուցչի դեպքում
իրական ցուցչի դեպքում  -ը կարելի է որոշել որպես
-ը կարելի է որոշել որպես  հաջորդականության սահման, որտեղ
հաջորդականության սահման, որտեղ  -ը
-ը  -ին ձգտող ռացիոնալ թիվ է։ Էքսպոնենտայի համար գոյություն ունեն նաև այլ սահմանում սահմանի օգնությամբ, օրինակ՝
-ին ձգտող ռացիոնալ թիվ է։ Էքսպոնենտայի համար գոյություն ունեն նաև այլ սահմանում սահմանի օգնությամբ, օրինակ՝
 ։
։
Հատկություններ

Ցուցչային ֆունկցիայի գրաֆիկը
Օգտագործելով  բնական լոգարիթմի ֆունկցիան, կարելի է ցուցչային ֆունկցիան արտահայտել կամայական դրական հիմքով էքսպոնենտայի միջոցով՝
բնական լոգարիթմի ֆունկցիան, կարելի է ցուցչային ֆունկցիան արտահայտել կամայական դրական հիմքով էքսպոնենտայի միջոցով՝
 ։
։
Այս կապը հնարավորություն է տալիս սահմանափակվել էքսպոնենտայի հատկության ուսումնասիրմամբ։ Անալիտիկ հատկություններ՝
 .
.
Մասնավորապես՝
Լոգարիթմական ֆունկցիա
Լոգարիթմական ֆունկցիա կոչվում է f (x) = log a x բանաձևով տրված ֆունկցիան, որտեղa–ն 1-ից տարբեր դրական թիվ է:
Լոգարիթմական ֆունկցիաների հիմնական հատկությունները.
- Ֆունկցիայի որոշման տիրույթը դրական կիսառանցքն է՝
D(F)=(0,∞)
1. Ֆունկիայի արժեքների բազմությունն ամբողջ թվային առանցքն է՝
- Ֆունկցիան մոնոտոն է իր որոշման տիրույթում: Այն աճող է, եթե a > 1 և նվազող` եթե 0< a < 1
- Ֆունկցիան 0 արժեքն ընդունում է x = 1 կետում
ա) a > 1 դեպքում ֆունկցիան բացասական է (0, 1) և դրական`
Միջակայքում
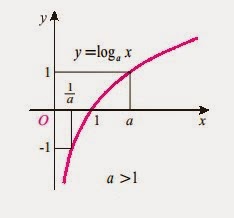
բ) 0< a < 1 դեպքում ֆունկցիան դրական է (0, 1) և բացասական`
Միջակայքում
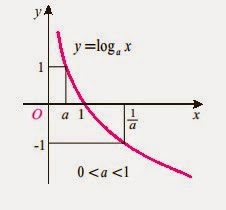
Միևնույն
հիմքով լոգարիթմական և ցուցչային ֆունկցիաները փոխհակադարձֆունկցիաներ են: Նրանցգրաֆիկները համաչափ են y = x ուղղի նկատմամբ: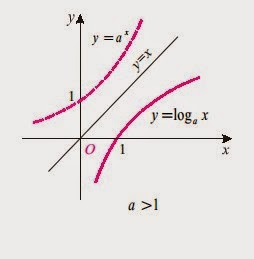
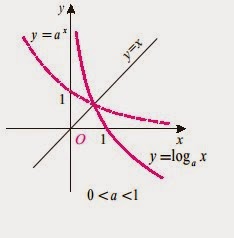
Օրինակներ
ՀԱՐԹԱՉԱՓՈՒԹՅՈՒՆ
Հարթաչափություն, երկրաչափության բաժին է, որնուսումնասիրում է մեկ հարթության պատկանող պատկերների(հարթ պատկերներ) հատկությունները։
Եռանկյուն
Եռանկյան տեսակներԿախված կողմերի երկարությունների փոխհարաբերությունից ևանկյունների մեծությունից, եռանկյունները լինում ենուղղանկյուն (անկյուններից մեկն ուղիղ է), բութանկյուն(անկյուններից մեկը բութ է), սուրանկյուն (բոլոր երեքանկյունները սուր են), հավասարակողմ կամ կանոնավոր (բոլոր երեք կողմերն իրարհավասար են) և հավասարասրուն (հավասար են գոնե երկուկողմերը)։
ՈւղղանկյունեռանկյունԵռանկյունը, որի անկյուններից մեկն ուղիղ է կոչվում էուղղանկյուն եռանկյուն: Ուղիղ անկյան դիմացի կողմը կոչվում է ներքնաձիգ, մյուսկողմերը` էջեր: Ուղղանկյուն եռանկյան սուր անկյունների գումարը 90° է: Ուղղանկյուն եռանկյան 30°-ի անկյան դիմացի էջը հավասար էներքնաձիգի կեսին: Ուղղանկյուն եռանկյան ուղիղ անկյան գագաթից տարվածմիջնագիծը հավասար է ներքնաձիգի կեսին: (Պյութագորասի թեորեմ) Ուղղանկյուն եռանկյան ներքնաձիգիքառակուսին հավասար է էջերի քառակուսիների գումարին: Ուղղանկյուն եռանկյանն արտագծած շրջանագծի կենտրոնըներքնաձիգի միջնակետն է, իսկ շառավիղը հավասար էներքնաձիգի կեսին: Ուղղանկյուն եռանկյան սուր անկյան սինուս է կոչվումհանդիպակաց էջի հարաբերությունը ներքնաձիգին: Ուղղանկյուն եռանկյան սուր անկյան կոսինուս է կոչվում կից էջիհարաբերությունը ներքնաձիգին: Ուղղանկյուն եռանկյան սուր անկյան տանգենս է կոչվումհանդիպակաց էջի հարաբերությունը կից էջին: Ուղղանկյուն եռանկյան սուր անկյան կոտանգենս է կոչվում կիցէջի հարաբերությունը հանդիպակաց էջին:
Հավասարակողմ եռանկյունԵռանկյունը, որի բոլոր կողմերը հավասար են կոչվում էհավասարակողմ կամ կանոնավոր եռանկյուն: Հավասարակողմ եռանկյան անկյունները 60° են: Հավասարակողմ եռանկյան նույն կողմին տարված միջնագիծը,կիսորդն ու բարձրությունը համընկնում են: Հավասարասրուն եռանկյուն Եռանկյունը կոչվում է հավասարասրուն, եթե նրա երկու կողմերըհավասար են: Հավասար կողմերը կոչվում են սրունքներ, երրորդ կողմը` հիմք: Հավասարասրուն եռանկյան հիմքին առընթեր անկյուններըհավասար են: Եթե հավասարասրուն եռանկյան անկյուններից որևէ մեկը 60° է,ապա այդ եռանկյունը հավասարակողմ եռանկյուն է: Հավասարասրուն եռանկյան հիմքին տարված բարձրությունը,կիսորդն ու միջնագիծը համընկնում են: Եթե եռանկյան երկու անկյունները հավասար են, ապաեռանկյունը հավասարասրուն է:
Եռանկյան գագաթից տարված բարձրություն է կոչվում այդգագաթից նրա դիմացի կողմը պարունակող ուղղին տարվածուղղահացը։
Եռանկյան բարձրությունները կամ նրանց շարունակություններըհատվում են մի կետում:
Եռանկյան գագաթից տարված կիսորդ է կոչվում եռանկյանանկյան կիսորդի այն հատվածը, որի միացնում է այդ գագաթը ևնրա դիմացի կողմի վրա գտնվող կետը։
Եռանկյան անկյան կիսորդը դիմացի կողմը բաժանում է կիցկողմերին համեմատական մասերի:
Եռանկյան կիսորդները հատվում են մի կետում:
Եռանկյան կիսորդների հատման կետը եռանկյանը ներգծածշրջանագծի կենտրոնն է:
Եռանկյան միջնագիծ է կոչվում այդ գագաթը և դիմացի կողմիմիջնակետը միացնող հատվածը։
Եռանկյան միջնագծերը հատվում են մի կետում, որըյուրաքանչյուր միջնագիծը բաժանում է 2:1 հարաբերությամբ,հաշված գագաթից:
Եռանկյունն իր միջնագծով բաժանվում է երկու հավասարամեծեռանկյունների:
Եռանկյան միջին գիծ է կոչվում նրա երկու կողմերիմիջնակետերը միացնող հատվածը։
Եռանկյան միջին գիծը զուգահեռ է նրա կողմերից մեկին ևհավասար է այդ կողմի կեսին:
Եռանկյան միջին գիծը եռանկյունը բաժանում է մասերի, որոնցմակերեսների հարաբերությունը 3 է:
Եռանկյան կողմերի միջնուղղահայացները հատվում են միկետում:
Եռանկյան կողմերի միջնուղղահայացների հատման կետըեռանկյանն արտագծած շրջանագծի կենտրոնն է:
Եռանկյունների հավասարությունԵռանկյունները հավասար են, եթե հավասար են նրանցհամապատասխան կողմերն ու համապատասխան անկյունները։
Եռանկյունների հավասարության հայտանիշները՝
- Եթե մի եռանկյան երկու կողմերը և նրանցով կազմված անկյունըհամապատասխանաբար հավասար են մյուս եռանկյան երկուկողմերին և նրանցով կազմված անկյանը, ապա այդպիսիեռանկյունները հավասար են։
- Եթե մի եռանկյան մի կողմը և նրան առընթեր անկյուններըհամապատասխանաբար հավասար են մյուս եռանկյան կողմին ևնրան առընթեր անկյուններին, ապա այդպիսի եռանկյուններըհավասար են։
- Եթե մի եռանկյան երեք կողմերը համապատասխանաբարհավասար են մյուս եռանկյան երեք կողմերին, ապա այդպիսիեռանկյունները հավասար են։
Եռանկյունների նմանությունԵռանկյունները նման են, եթե այդ եռանկյուններիհամապատասխան անկյունները հավասար են, իսկհամապատասխան կողմերի հարաբերությունը նույնն է։ Այսինքն∆ABC և ∆A1B1C1 նման եռանկյունների միջև
∏ = ∏ = ∏, ∠A=∠A1, ∠B=∠B1, ∠C=∠C1։
Եռանկյունների նմանության հիմնական թեորեմներն են՝
- Երկու եռանկյուններ նման են, եթե նրանցից մեկի երկուանկյունները համապատասխանաբար հավասար են մյուսի երկուանկյուններին։
- Երկու եռանկյուններ նման են, եթե նրանցից մեկի երկու կողմերըհամեմատական են մյուսի երկու կողմերին և այդ կողմերովկազմված անկյունները հավասար են։
- Երկու եռանկյուններ նման են, եթե մեկի կողմերըհամեմատական են մյուսի կողմերին։
Եռանկյան մակերեսԵռանկյան մակերեսի ամենատարածված հավասարումն է նրակողմի և այդ կողմին տարված բարձրության արտադրյալի կեսը։
Եռանկյան մակերեսը հավասար է երկու կողմերի և նրանցովկազմված անկյան սինուսի արտադրյալի կեսին:
Եռանկյան մակերեսը հավասար է կողմերի արտադրյալի և նրանարտագծած շրջանագծի շառավղի քառապատիկիհարաբերությանը:
Եռանկյան մակերեսի կարելի է հաշվել նաև Հերոնի բանաձևով:
Քառանկյուններ
Քառակուսի
Քառակուսի է կոչվում այն ուղղանկյունը, որի բոլոր կողմերըհավասար են:
Քառակուսու անկյունագծերը. հավասար են, փոխուղղահայացեն, հատման կետում կիսվում են,
կիսում են քառակուսու անկյունները:
Քառակուսու մակերեսը հավասար է կողմի քառակուսուն:
Քառակուսու մակերեսը հավասար է անկյունագծի քառակուսուկեսին:
ՇեղանկյունԱյն զուգահեռագիծը, որի բոլոր կողմերը հավասար են, կոչվում էշեղանկյուն:
Շեղանկյան անկյունագծերը փոխուղղահայաց են և կիսում եննրա անկյունները:
Շեղանկյան մակերեսը հավասար է նրա հիմքի և բարձրությանարտադըրյալին:
Շեղանկյան մակերեսը հավասար է նրա անկյունագծերիարտադրյալի կեսին:
Շեղանկյան մակերեսը հավասար է նրա կողմի քառակուսու ևանկյան սինուսի արտադրյալին:
Շեղանկյան բարձրությունը հավասար է նրան ներգծածշրջանագծի տրամագծին:
ՈւղղանկյունԱյն զուգահեռագիծը, որի բոլոր անկյունները ուղիղ են, կոչվում էուղղանկյուն: Ուղղանկյան անկյունագծերը հավասար են: Եթե զուգահեռագծի անկյունագծերը հավասար են, ապազուգահեռագիծը ուղղանկյուն է: Ուղղանկյան մակերեսը հավասար է կից կողմերի արտադրյալին: Ուղղանկյան մակերեսը հավասար է անկյունագծի քառակուսու ևանկյունագծերի կազմած անկյան սինուսի արտադրյալի կեսին:
ԶուգահեռագիծԶուգահեռագիծ է կոչվում է այն քառանկյունը, որի հանդիպակացկողմերը զույգ առ զույգ զուգահեռ են:
Զուգահեռագծի անկյունների գումարը 360° է: Զուգահեռագծի որևէ կողմին առընթեր անկյունների գումարը180° է: Զուգահեռագծի հանդիպակաց կողմերը հավասար են:Զուգահեռագծի հանդիպակաց անկյունները հավասար են: Զուգահեռագծի անկյունագծերի քառակուսիների գումարըհավասար է բոլոր կողմերի քառակուսիների գումարին: Եթե քառանկյան երկու կողմերը հավասար և զուգահեռ են, ապաքառանկյունը զուգահեռագիծ է: Եթե քառանկյան հանդիպակաց կողմերը զույգ առ զույգհավասար են, ապա քառանկյունը զուգահեռագիծ է: Եթե քառանկյան անկյունագծերը հատվում և հատման կետովկիսվում են, ապա քառանկյունը զուգահեռագիծ է: Զուգահեռագծի մակերեսը հավասար է նրա հիմքի ևբարձրության արտադրյալին: Զուգահեռագծի մակերեսը հավասար է կից կողմերի և նրանցովկազմված անկյան սինուսի արտադրյալին:
ՍեղանՍեղան է կոչվում այն քառանկյունը, որի երկու կողմերը զուգահեռ են, իսկ մյուս երկու կողմերը` ոչ: Զուգահեռ կողմերը կոչվում են հիմքեր, իսկ մյուս կողմերը`կողմնային կողմեր:
Սեղանը կոչվում է հավասարասրուն, եթե նրա կողմնային կողմերը (սրունքները) հավասար են: Հավասարասրուն սեղանի յուրաքանչյուր հիմքին առընթեր անկյունները հավասար են: Անկյունագծերը նույնպես հավասար են:
Եթե սեղանի հիմքին առընթեր անկյունները հավասար են, ապա սեղանը հավասարասրուն է: Եթե սեղանի անկյունագծերը հավասար են, ապա սեղանը հավասարասրուն է:
Շրջանագծին ներգծած սեղանը հավասարասրուն է: Սեղանը, որի անկյուններից մեկն ուղիղ է, կոչվում է ուղղանկյուն սեղան: Սեղանի միջին գիծը զուգահեռ է սեղանի հիմքերին և հավասար է նրանց կիսագումարին: Սեղանի մակերեսը հավասար է միջին գծի և բարձրության արտադրյալին:
Սեղանի մակերեսը հավասար է նրա անկյունագծերի և նրանցով կազմված անկյան սինուսի արտադրյալի կեսին:
Եթե սեղանին հնարավոր է ներգծել շրջանագիծ, ապա այդ շրջանագծի շառավիղը հավասար է սեղանի բարձրության կեսին:
Շրջանագիծ, շրջան
Շրջանագիծ է կոչվում հարթության այն կետերից բաղկացած երկրաչափական պատկերը, որոնք տրված կետից (կենտրոնից) գտնվում են տրված հեռավորության (շառավիղ) վրա: Շրջանագծի երկու կետերը միացնող հատվածը կոչվում է լար:
Շրջանագծի կենտրոնով անցնող լարը կոչվում է տրամագիծ: Շրջանագծի երկու կետերի միջև ընկած մասը կոչվում է աղեղ: Ուղիղը, որը շրջանագծի հետ ունի միայն մեկ ընդհանուր կետ, կոչվում է շրջանագծի շոշափող: Շրջանագծի շոշափողն ուղղահայաց է շոշափման կետից տարված շառավղին:
Եթե ուղիղն անցնում է շառավղի` շրջանագծի վրա գտնվող ծայրակետով և ուղղահայաց է այդ շառավղին, ապա այն շոշափող է: Միևնույն կետից շրջանագծին տարված շոշափողների հատվածները հավասար են և կազմում են հավասար անկյուններ այդ կետով և շրջանագծի կենտրոնով անցնող ուղղի հետ: Լարին ուղղահայաց տրամագիծը (շառավիղը) կիսում է այդ լարը և նրանով ձգված աղեղը: Այն անկյունը, որի գագաթը շրջանագծի կենտրոնն է, կոչվում է կենտրոնական անկյուն:
Շրջանագծի աղեղի աստիճանային չափը այն կենտրոնական անկյան աստիճանային չափն է, որը հենված է այդ աղեղի վրա: Այն անկյունը, որի գագաթը գտնվում է շրջանագծի վրա, իսկ կողմերը հատում են շրջանագիծը, կոչվում է ներգծյալ անկյուն: Ներգծյալ անկյունը չափվում է այն աղեղի կեսով, որի վրա հենված է:
Միևնույն աղեղի վրա հենված ներգծյալ անկյունները հավասար են: Տրամագծի վրա հենված ներգծյալ անկյունը ուղիղ է: Շրջանագծի զուգահեռ լարերի միջև պարփակված աղեղների աստիճանային չափերը հավասար են:
Անկյունը, որի գագաթը շրջանագծից դուրս է, իսկ կողմերը հատում են շրջանագիծը, չափվում է հատողների մեջ պարփակված աղեղների կիսատարբերությամբ: Հատվող լարերով կազմված անկյունը չափվում է նրանց անջատած աղեղների կիսագումարով: Շոշափողով և լարով կազմված անկյունը չափվում է նրանց մեջ պարփակված աղեղի կեսով:
Եթե շրջանագծի երկու լարերը հատվում են, ապա լարերից մեկի հատվածների արտադրյալը հավասար է մյուս լարի հատվածների արտադրյալին:
Երկու շրջանագծեր ունեն արտաքին շոշափում, եթե նրանք ունեն միայն մեկ ընդհանուր կետ և կենտրոնները գտնվում են այդ կետի տարբեր կողմերում: Արտաքին շոշափման դեպքում շրջանագծերի կենտրոնների հեռավորությունը հավասար է շրջանագծերի շառավիղների գումարին:
Շրջանի այն մասը, որը սահմանափակված է աղեղով և աղեղի ծայրակետերը շրջանի կենտրոնին միացնող երկու շառավիղներով, կոչվում է սեկտոր:
Շրջանի այն մասը, որը սահմանափակված է աղեղով և աղեղի ծայրակետերը միացնող լարով, կոչվում է սեգմենտ:
ՏԱՐԱԾԱՉԱՓՈՒԹՅՈՒՆ
Գլան
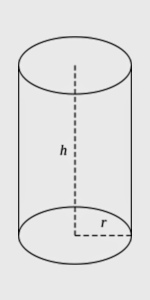
V = S
հ*H = πR
2H
S
կ = 2πRH
S
լր = S
կ + 2S
հ = 2πRH + 2πR
2 =>
S
լր = 2πR(H + R)
Կոն
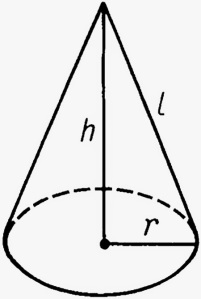
V = 1/3 S
h*H = 1/3 πR
2H
Sկ = πRl
Sլր = Sկ + Sհ = πRl + πR2 =>
Sլր = πR(l + R)
Հատած կոն
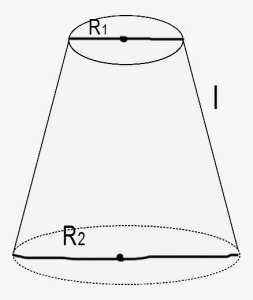 V = 1/3
V = 1/3 π
H (R12 + R22 + R1R2) = 1/3 H(S1 + S2 +√(S1+S2) )
Sկ = π(R
1 + R
2)l
S
լր = S
կ + S1 + S
2 =>
S
լր = π(R
1 + R
2)l + πR
12 + πR
22l
2 = H
2 + (R
1 – R
2)
2H = lsinα = (R
1 – R
2)tgα
Ուղղանկյունանիստ
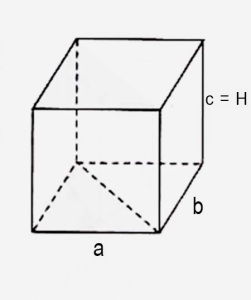 V = Sհ*
V = Sհ*H = a
*b
*c (c = H)
S
կ = P
h * H = 2c(a+b)
S
լր = 2(ab + bc + ac)
Խորանարդ
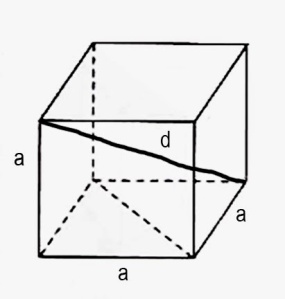
V = a*a*a = a3
Sկ = 4a
2S
լր = 6a2
d = 3a2
Բուրգ
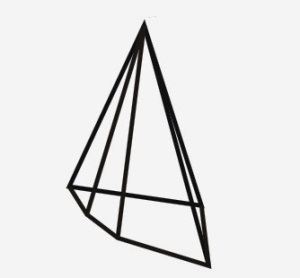
V= 1/3 S
հ*H
S
լր = S
կ + S
հԿանոնավոր բուրգ
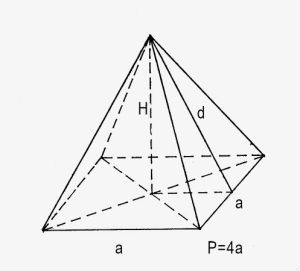
V = 1/3 Sհ*H
Sկ = 1/2 Pd
Sլր = 1/2 Pd + Sհ



 Անտարկտիդան մեր մոլորակի՝ մեծությամբ հինգերորդ մայրցամաքն է։ Մակերեսը կազմում է շուրջ 14 մլն. կմ²։ Գտնվում է Երկրագնդի ծայր հարավում և ամբողջովին սառցապատ է։ Ողողվում է Ատլանտյան, Հնդկական և Խաղաղ օվկիանոսների ջրերով, որոնք մշտապես ծածկված են լողացող սառցալեռներով (այսբերգներով)։
Անտարկտիդան մեր մոլորակի՝ մեծությամբ հինգերորդ մայրցամաքն է։ Մակերեսը կազմում է շուրջ 14 մլն. կմ²։ Գտնվում է Երկրագնդի ծայր հարավում և ամբողջովին սառցապատ է։ Ողողվում է Ատլանտյան, Հնդկական և Խաղաղ օվկիանոսների ջրերով, որոնք մշտապես ծածկված են լողացող սառցալեռներով (այսբերգներով)։ Անտարկտիդան գրեթե ամբողջությամբ ծածկված է հզոր սառցադաշտերով, որոնց միջին հզորությունը մոտ 2000 մ. է, իսկ առավելագույնը՝ 4500 և ավելի։ Այստեղ է գտնվում Երկրագնդի սառցադաշտերի 90%-ը։ Եթե սառույցը փռենք ամբողջ երկրի մակերևույթի վրա, ապա վերջինս կծածկվի 40 մ. հաստության սառցաշերտով, իսկ եթե այն հալվի, ապա Համաշխարհային օվկիանոսի մակարդակը կբարձրանա 60 մ.-ով։ Անտարկտիդայի ներքին շրջաններից սառույցը դանդաղ սահում է ծայրամասեր ու կոտրվելով ընկնում է ծով՝ առաջացնելով վիթխարի սառցասարեր, որոնք կոչվում են այսբերգներ։ Անտարկտիդայի շրջակա ջրերում հանդիպել են մինչև 170 կմ. երկարության և 70 – 100 մ. բարձրության սեղանաձև այսբերգներ։
Անտարկտիդան գրեթե ամբողջությամբ ծածկված է հզոր սառցադաշտերով, որոնց միջին հզորությունը մոտ 2000 մ. է, իսկ առավելագույնը՝ 4500 և ավելի։ Այստեղ է գտնվում Երկրագնդի սառցադաշտերի 90%-ը։ Եթե սառույցը փռենք ամբողջ երկրի մակերևույթի վրա, ապա վերջինս կծածկվի 40 մ. հաստության սառցաշերտով, իսկ եթե այն հալվի, ապա Համաշխարհային օվկիանոսի մակարդակը կբարձրանա 60 մ.-ով։ Անտարկտիդայի ներքին շրջաններից սառույցը դանդաղ սահում է ծայրամասեր ու կոտրվելով ընկնում է ծով՝ առաջացնելով վիթխարի սառցասարեր, որոնք կոչվում են այսբերգներ։ Անտարկտիդայի շրջակա ջրերում հանդիպել են մինչև 170 կմ. երկարության և 70 – 100 մ. բարձրության սեղանաձև այսբերգներ։ Առափնյա շրջաններում և կղզիներում աճում են մամուռներ, քարաքոսեր, ջրիմուռներ։ Անտարկտիդայի կլիմայական պայմաններում հարուստ բուսականություն չի կարող լինել։ Սառեցող ջերմաստիճանը, հողի ցածր որակը, խոնավությունը և արևի ճառագայթների պակասը կանխում են բույսերի աճը։ Հետևաբար, բուսակունության բազմազանությունը շատ աղքատիկ է և տարածում չի գտել։ Անտեսելով բուսական ծագում չունեցող օրգանիզմները (ծովալոռերը և սնկերը, այդ թվում նաև քարաքոսային տեսակները), մայրցամաքի բուսականությունը հիմնականում կազմված է բրիոֆիտներից (մամուռի մոտավորապես 100 տեսակ, ինչպես նաև երիժնակի 25 տեսակ), ծաղկող բույսերի ընդամենը երկու տեսակ, որոնք հայտնաբերվել են Անտարկտիդայի թերակղզում՝ Դեսցհապսիա Անտարկտիդա (Անտարկտիկ մազաբույս)։ Ծաղկունք է տեղի ունենում միայն ամռանը՝ ընդամենը մի քանի շաբաթվա ընթացքում:
Առափնյա շրջաններում և կղզիներում աճում են մամուռներ, քարաքոսեր, ջրիմուռներ։ Անտարկտիդայի կլիմայական պայմաններում հարուստ բուսականություն չի կարող լինել։ Սառեցող ջերմաստիճանը, հողի ցածր որակը, խոնավությունը և արևի ճառագայթների պակասը կանխում են բույսերի աճը։ Հետևաբար, բուսակունության բազմազանությունը շատ աղքատիկ է և տարածում չի գտել։ Անտեսելով բուսական ծագում չունեցող օրգանիզմները (ծովալոռերը և սնկերը, այդ թվում նաև քարաքոսային տեսակները), մայրցամաքի բուսականությունը հիմնականում կազմված է բրիոֆիտներից (մամուռի մոտավորապես 100 տեսակ, ինչպես նաև երիժնակի 25 տեսակ), ծաղկող բույսերի ընդամենը երկու տեսակ, որոնք հայտնաբերվել են Անտարկտիդայի թերակղզում՝ Դեսցհապսիա Անտարկտիդա (Անտարկտիկ մազաբույս)։ Ծաղկունք է տեղի ունենում միայն ամռանը՝ ընդամենը մի քանի շաբաթվա ընթացքում: Ջրերը հարուստ են Պլանկտոնով՝ բուսական և կենդանական մանր օրգանիզմներով, որոնք սննդի աղբյուր են հանդիսանում կետերի, փոկերի, դելֆինների, ձկների, թռչունների համար։ Այստեղ ապրում են մի քանի տեսակի կետազգիներ, որոնցից նշանավոր է Կապույտ կետը (աշխարհի ամենախոշոր կենդանին), ինչպես նաև կաշալոտը (վիշապաձուկ)։
Ջրերը հարուստ են Պլանկտոնով՝ բուսական և կենդանական մանր օրգանիզմներով, որոնք սննդի աղբյուր են հանդիսանում կետերի, փոկերի, դելֆինների, ձկների, թռչունների համար։ Այստեղ ապրում են մի քանի տեսակի կետազգիներ, որոնցից նշանավոր է Կապույտ կետը (աշխարհի ամենախոշոր կենդանին), ինչպես նաև կաշալոտը (վիշապաձուկ)։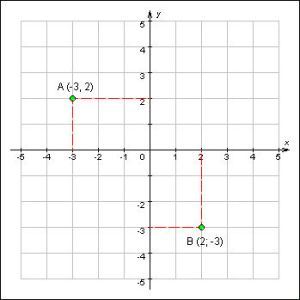




 տեսքի
տեսքի  -ն կոչվում է ցուցչի հիմք, իսկ
-ն կոչվում է ցուցչի հիմք, իսկ  -ը՝ ցուցչի աստիճան։
-ը՝ ցուցչի աստիճան։ , մտցվել է Լեյբնիցի կողմից
, մտցվել է Լեյբնիցի կողմից  թիվը։ Այդպիսի ֆունկցիան կոչվում է էքսպոնենտային (իրական կամ կոմպլեքս)։
թիվը։ Այդպիսի ֆունկցիան կոչվում է էքսպոնենտային (իրական կամ կոմպլեքս)։ ։ Այդ դեպքում
։ Այդ դեպքում  -ը որոշվում է հետևյալ կանոններով՝
-ը որոշվում է հետևյալ կանոններով՝ , ապա
, ապա ![a^x= \sqrt[n]{a^m}](https://i2.wp.com/upload.wikimedia.org/math/5/9/b/59bb51c4bbf9bb3f0c594b414317e599.png) ։
։ և
և  , ապա
, ապա  ։
։ -ի արժեքը որոշված չէ։
-ի արժեքը որոշված չէ։ և
և  , ապա
, ապա ։
։ -ի դեպքում որոշված չէ։
-ի դեպքում որոշված չէ։ հաջորդականության սահման, որտեղ
հաջորդականության սահման, որտեղ  -ը
-ը  ։
։




 բնական լոգարիթմի ֆունկցիան, կարելի է ցուցչային ֆունկցիան արտահայտել կամայական դրական հիմքով էքսպոնենտայի միջոցով՝
բնական լոգարիթմի ֆունկցիան, կարելի է ցուցչային ֆունկցիան արտահայտել կամայական դրական հիմքով էքսպոնենտայի միջոցով՝ ։
։ .
.